Compute right hand side for diffusion terms. More...

#include "pluto.h"

Functions
double	ParabolicRHS (const Data d, Data_Arr dU, double dt, Grid grid)

Detailed Description

The ParabolicRHS function computes the right hand side, in conservative or divergence form, of the parabolic (diffusion) operators only:

$\pd{q}{t} = - \nabla\cdot\Big(D\nabla q\Big)$

Here q is a generic quantity (like momentum, magnetic field or total energy) and 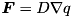$\vec{F} = D\nabla q$ is the corresponding flux computed elsewhere. Contributions may simultaneously come from viscosity, magnetic resistivity and thermal conduction for which the flux functions are computed in the function ViscousFlux(), ResistiveFlux() or TC_Flux()).

This function is intended for operator split algorithms (STS, RKC) solving for the parabolic part of the equations.

This function also computes the inverse diffusion time step by adding, for each diffusion equation, contributions coming from different directions:

$\Delta t_{p}^{-1} = \max\left[\frac{\eta_{i+\HALF} + \eta_{i-\HALF}}{2\Delta x^2} + \frac{\eta_{j+\HALF} + \eta_{j-\HALF}}{2\Delta y^2} + \frac{\eta_{k+\HALF} + \eta_{k-\HALF}}{2\Delta z^2}\right]$

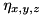where $\eta_{x,y,z}$ are the diffusion coefficients available at cell interfaces in the three directions, respectively, and the maximum is taken over the local processor grid.

Date: Oct 29, 2012

Authors: A. Mignone (migno.nosp@m.ne@p.nosp@m.h.uni.nosp@m.to.i.nosp@m.t)
P. Tzeferacos

Function Documentation

double ParabolicRHS	(	const Data *	d,
		Data_Arr	dU,
		double	dt,
		Grid *	grid
	)

Parameters

[in]	V	3D array containing primitive variables
[out]	dU	3D array containing the conservative right hand sides
[in]	dt	the time step
[in]	grid	a pointer to an array of Grid structure

Returns: On output it returns the maximum diffusion coefficients among all dissipative term over the local processor grid.

Functions

Detailed Description

Function Documentation