Advance equations using Corner Transport Upwind (CTU). More...

#include "pluto.h"

Functions
static void	CTU_CT_Source (double , double , double *, double , int, int, Grid *)

int	Unsplit (const Data d, Riemann_Solver Riemann, Time_Step Dts, Grid grid)

Detailed Description

Implement the dimensionally unsplit, Corner Transport Upwind method (CTU) of Colella. It consists of

A predictor step :

start from cell center values of V and compute time-centered interface states using either HANCOCK or CHARACTERISTIC_TRACING:
$V^{n+\HALF}_{i,\pm} = V^n_{i,\pm} + \pd{V}{t}\frac{\Delta t}{2}$
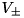Store the resulting states by converting $V_\pm$ in $U_\pm$ (= UP, UM). Normal (n) and trasnverse (t) indexes for this step should span $n \in [n_{\rm beg} - 1, n_{\rm end} + 1]$ , $t \in [t_{\rm beg} - 1, t_{\rm end} + 1]$ for cell-centered schemes and $n \in [n_{\rm beg} - 2, n_{\rm end} + 2]$ , $t \in [t_{\rm beg} - 2, t_{\rm end} + 2]$ for staggered MHD.
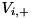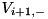Solve Riemann problems between $V_{i,+}$ and $V_{i+1,-}$ and store the flux difference in RHS.
Compute cell and time-centered values UH = U + dt/2*RHS with index range $n \in [n_{\rm beg}, n_{\rm end}]$ , $t \in [t_{\rm beg}, t_{\rm end}]$ for cell-centered schemes and $n \in [n_{\rm beg}-1, n_{\rm end}+1]$ , $t \in [t_{\rm beg}-1, t_{\rm end}+1]$ for staggered MHD.

A corrector step :

correct left and right states UP and UM computed in the previous step by adding the transverse RHS contribution, e.g. 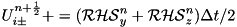$U^{n+\HALF}_{i\pm} += ({\cal RHS}^n_y + {\cal RHS}^n_z)\Delta t/2$ . This step should cover $[n_{\rm beg}-1, n_{\rm end} + 1]$ , $[t_{\rm beg}, t_{\rm end}]$ for cell-centered MHD and $[n_{\rm beg}-2, n_{\rm end} + 2]$ , $[t_{\rm beg}-1, tend+1]$ for staggered MHD.

Solve a normal Riemann problem with left and right states UP and UM, get RHS and evolve to final stage, 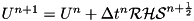$U^{n+1} = U^n + \Delta t^n {\cal RHS}^{n+\HALF}$

This integrator performs an integration in the ghost boundary zones, in order to recover appropriate information to build the transverse predictors.

Note: If explicit parabolic flux have to be included, the predictor step is modified by computing the RHS from 1st order states at t^n. This allows to obtain space and time centered states in one row of boundary zones required during the following corrector step.

References

"The Piecewise Parabolic Method for Multidimensional Relativistic Fluid Dynamics"
Mignone, A.; Plewa, T.; Bodo, G. ApJS (2005), 160..199M
"An unsplit Godunov method for ideal MHD via constrained transport"
Gardiner & Stone, JCP (2005), 205, 509

"A second-order unsplit Godunov scheme for cell-centered MHD: the CTU-GLM scheme"
Mignone & Tzeferacos JCP (2010), 229, 2117

Authors: A. Mignone (migno.nosp@m.ne@p.nosp@m.h.uni.nosp@m.to.i.nosp@m.t)
P. Tzeferacos (petro.nosp@m.s.tz.nosp@m.efera.nosp@m.cos@.nosp@m.ph.un.nosp@m.ito..nosp@m.it)

Date: Oct 1, 2012

Function Documentation

void CTU_CT_Source	(	double **	v,
		double **	up,
		double **	um,
		double *	dtdV,
		int	beg,
		int	end,
		Grid *	grid
	)

static

Add source terms to conservative left and right states obtained from the primitive form of the equations. The source terms are:

m += dt/2 * B * dbx/dx
Bt += dt/2 * vt * dbx/dx (t = transverse component)
E += dt/2 * v*B * dbx/dx

These terms are NOT accounted for when the primitive form of the equations is used (see Gardiner & Stone JCP (2005), Crockett et al. JCP(2005)). This is true for both the Charactheristic Tracing AND the primitive Hancock scheme when the constrained transport is used, since the resulting system is 7x7. To better understand this, you can consider the stationary solution rho = p = 1, v = 0 and Bx = x, By = -y. If these terms were not included the code would generate spurious velocities.

int Unsplit	(	const Data *	d,
		Riemann_Solver *	Riemann,
		Time_Step *	Dts,
		Grid *	grid
	)

Advance equations using the corner transport upwind method (CTU)

Parameters

[in,out]	d	pointer to Data structure
[in]	Riemann	pointer to a Riemann solver function
[in,out]	Dts	pointer to time step structure
[in]	grid	pointer to array of Grid structures

Functions

Detailed Description

Function Documentation